【三角関数】積和の公式～sinαcosβなどの解法

電気電子系の勉強を行う上で、昔学校で習った数学の知識が微妙に必要なことがありますので、せっかくだから少し詳しく学び直し、まとめてみました。
『なんでその定理が成り立つのか』という理由まで調べてみたものもあったりなかったりします。

今回は、「積和の公式」についての説明です。

１．積和の公式とは？
２．sinαsinβの証明
３．sinαcosβの証明
４．cosαcosβの証明

１．積和の公式とは？

三角関数の積和の公式とは、左辺が積になっていて、右辺が和になっている公式を指します。

つまり、sinαsinβ、sinαcosβ、cosαcosβの公式です。

この辺から公式の見た目がゴツゴツしてきて単純に覚えるのが困難になってきますので、しっかりと導き方を理解して記憶に定着させるように頑張りましょう。
やり方さえわかってしまえばすぐに導き出せます。
別に業務では直接的に役に立たないけど。

肝心の積和の公式は以下の3式となります。

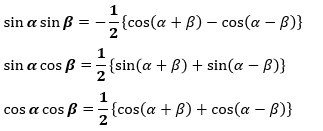
どうしてこうなるかは次の項から証明していきますね。

まずはsinαsinβの証明から始めます。
ここでは、cosの加法定理であるcos(α±β)=cosαcosβ∓sinαsinβの公式を使用していきます。
使用すると言っても、引き算するだけなんですけどね。

cos(α+β)－cos(α－β)
=(cosαcosβ－sinαsinβ)－(cosαcosβ+sinαsinβ)
=－2sinαsinβ

後は－2を移項するだけで公式が導き出せます。

－2sinαsinβ=cos(α+β)－cos(α－β)

sinαsinβ=－{cos(α+β)－cos(α－β)}/2

次はsinαcosβの証明です。
ここでは、sinの加法定理であるsin(α±β)=sinαcosβ±cosαsinβの公式を使用していきます。

sin(α+β)+sin(α－β)
=(sinαcosβ+cosαsinβ)+(sinαcosβ－cosαsinβ)
=2sinαcosβ

後は2を移項するだけで公式が導き出せます。

2sinαcosβ=sin(α+β)+sin(α－β)

sinαcosβ={sin(α+β)+sin(α－β)}/2

最後にcosαcosβの証明です。
ここまでの流れ的に大体何をするかは想像できそうですよね(笑)
ここでは、cosの加法定理であるcos(α±β)=cosαcosβ∓sinαsinβの公式を使用していきます。

cos(α+β)+cos(α－β)
=(cosαcosβ－sinαsinβ)+(cosαcosβ+sinαsinβ)
=2cosαcosβ

後は2を移項するだけで公式が導き出せます。

2cosαcosβ=cos(α+β)+cos(α－β)

cosαcosβ={cos(α+β)+cos(α－β)}/2

積和の公式の証明は以上です。簡単ですね。

三角関数の積和の公式が必要になったら加法定理を適当に足し引きしてみれば公式が導き出せると覚えておけば公式自体は別に覚える必要はないんです。

以上、「積和の公式」についての説明でした。

【基礎から学ぶ三角関数】