今回は、「関数同士が掛け算になっている場合の微分」についての説明です。
1.関数同士が掛け算になっている場合の微分
実際に使う機会があるかは不明ですが、数学の問題上では関数同士が掛け算になっているものを微分する問題が出現します。
今回はそんな場合の解法と関係式の導き方を説明していきます。
まずは結論から書いていきますね。
f(x)とg(x)という関数があったとして、それらの積を微分する場合は以下のような関係になります。
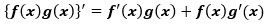
片方の関数を微分したものにもう片方の関数をそのまま掛けたもの同士を足し合わせた結果になるわけです。
式だけ見てもイメージできないので、実際に計算してみましょう。
f(x)=x+1、g(x)=2x+1だった場合は以下のようになります。
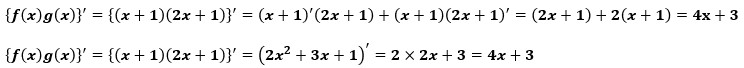
関係式を利用したものが上段、確認として関数の掛け算を計算した上で微分してみたものが下段です。
微分した結果が同じなので、この関係式が成り立っていることがわかりましたね。
2.関係式の導き方
覚える必要があるかは微妙なところですが、どうやってその関係式を導き出しているのかを記述していきます。
f(x)という関数を微分する場合の定義は以下のようになっていました。
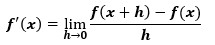
この定義に則ると、関数同士の掛け算の場合は以下のようになります。
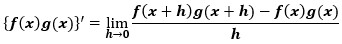
このままの形ではどう計算すればいいかわかりませんので、式を変形させていきましょう。
分子に“f(x)g(x+h)-f(x)g(x+h)”を付け足してみます。
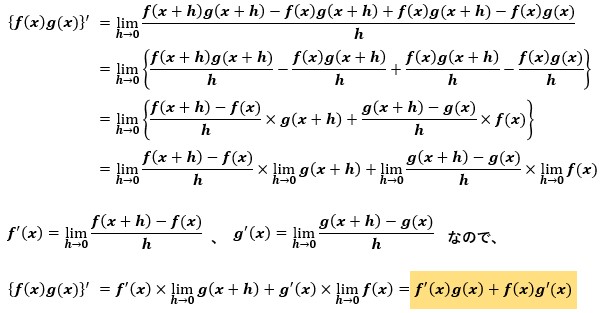
これで関係式を導くことができました。
最初に分子へ“f(x)g(x+h)-f(x)g(x+h)”を足そうと考えるのが変態染みてますよね。
以上、「関数同士が掛け算になっている場合の微分」についての説明でした。
【基礎から学ぶ微分】
