【三角関数】余弦定理～三角形の角と各辺の関係

電気電子系の勉強を行う上で、昔学校で習った数学の知識が微妙に必要なことがありますので、せっかくだから少し詳しく学び直し、まとめてみました。
『なんでその定理が成り立つのか』という理由まで調べてみたものもあったりなかったりします。

今回は、「余弦定理」についての説明です。

１．余弦定理とは？
２．余弦定理の証明

１．余弦定理とは？

正弦定理は「三角形のある角(のsin)と、その角と向かい合う辺の間に成り立っている関係式」のことを指していました。
正弦波はsin波のことなので、正弦の定理はsinに関する定理なわけです。

正弦の定理があるように、余弦の定理も存在します。

余弦定理は「三角形のある角(のcos)と、三角形を形成する各辺の間に成り立っている関係式」のことを指しています。

実際に図を見ながらイメージしてみましょう。

図1のように三角形があったとして、角Aと向かい合う辺BC、角Bと向かい合う辺AC、角Cと向かい合う辺ABがあります。
これらには以下のような関係が成り立っています。

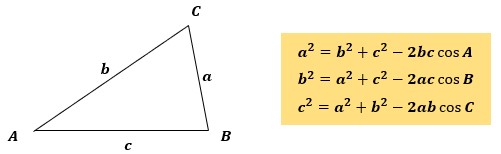
この関係式が余弦定理です。

abcの位置が入れ替わるだけの関係式なので、一度覚えてしまえば忘れにくい関係式かと思います。

では、なぜ余弦定理が成り立つのか証明していきます。

まず、どの角を対象にしても構わないので、角から対辺に垂線を引きます。
ここでは角Cから垂線を引いてみますね。

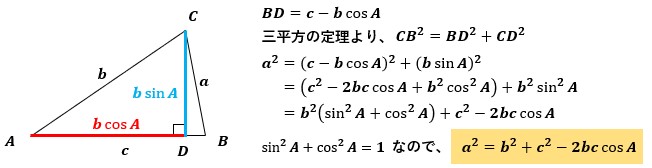
すると、△ACDと△BCDという直角三角形が2つできます。
この直角三角形に対して三平方の定理を適用して余弦定理を導き出します。

△BCDに着目して辺BD及び辺CDをaを用いずに表すと、BD=c-bcosA、CD=bsinAになります。
三平方の定理より、直角三角形の斜辺の二乗=縦辺の二乗+横辺の二乗になることがわかっているので、計算をしていくとa²=b²+c²-2bccosAが求まります。

余弦定理の他の2式に関しては、角Aから対辺BCに垂線を引いた場合と角Bから対辺ACに垂線を引いた場合についても同様に考えていくことで求めることが可能です。

実際に計算してみると記憶に定着しやすいので、試しに計算してみることをおすすめします。

以上、「余弦定理」についての説明でした。

【基礎から学ぶ三角関数】