今回は、「正弦定理」についての説明です。
1.正弦定理とは?
正弦定理とは、三角形の内角の正弦(sin)とその対辺の長さの比と外接円の半径の関係を表した定理です…というニュアンスの説明がその辺のサイトやWikipediaに出てきます。
この説明では初見の人は何を言っているのかわからなくて混乱すると思うので、「三角形のある角と、その角と向かい合う辺の間にはとある関係が成り立っていますよ」という内容をまとめたものと考えてください。
実際に図を見ながらイメージしてみましょう。
図1のように三角形があったとして、角Aと向かい合う辺BC、角Bと向かい合う辺AC、角Cと向かい合う辺ABがあります。
これらには図1右のような関係が成り立っています。
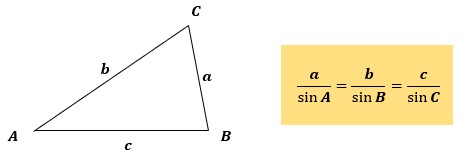
この関係式が正弦定理です。
つまり、sin(正弦)に関係する定理だから正弦定理という名前になっているだけです。
…なんで”三角形の内角の正弦(sin)”とかいうよくわからなくなるような言い回しするんですかね?
また、この三角形の外接円の半径Rと正弦定理の間には以下のような関係があります。

ここまで含めて正弦定理と呼ぶような気がしますが、実際のところどうなのかはよくわかっていません。
教科書を信じてください。(紛失済)
2.正弦定理の証明
では、なぜ正弦定理が成り立つのか証明していきます。
まず、どの角を対象にしても構わないので、角から対辺に垂線を引きます。
ここでは角Cから垂線を引いてみますね。
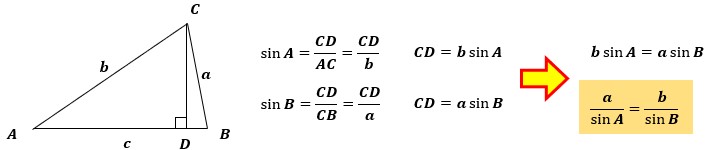
すると、△ACDと△BCDという直角三角形が2つできます。
これらの直角三角形からsinAとsinBを求めて式を変形すると、a/sinA=b/sinBが求まります。
これで正弦定理の左半分の証明が済みました。
ここまでの説明で勘が良い人は気づいたかもしれませんが、角Aから対辺BCに垂線を引いた場合と角Bから対辺ACに垂線を引いた場合についても同様に考えて照らし合わせると、a/sinA=b/sinB=c/sinCが成り立つことがわかります。
なのでその辺りの説明は割愛しまして、それらが「=2R」になる理由について考えていきます。
まず、点Bと外接円の中心を通る直線を引き、その直線と外接円との交点をEとします。
この点Eと点Aを結んで△AEBを作ります。
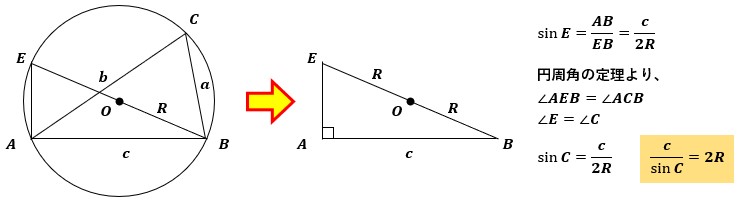
この時、円周角の定理より、∠EAB=90°、∠AEB=∠ACBになっていることがわかります。
(円周角の定理はいつかまとめると思います。)
△AEBを抜き出して考えてみると、辺EB=2R、辺AB=cであることが確定していますので、sinE=c/2Rとなります。
∠AEB=∠ACBということは、∠E=∠C、sinE=sinCが成り立っているので、式の形を整理するとc/sinC=2Rという関係が導き出せます。
a/sinA=b/sinB=c/sinCになることは既にわかっているので、a/sinA=b/sinB=c/sinC=2Rも成り立つわけです。
ちなみに、点Aと外接円の中心を通る直線を引いた場合と点Cと外接円の中心を通る直線を引いた場合を考えても同じように求めることが可能です。
以上、「正弦定理」についての説明でした。
【基礎から学ぶ三角関数】
◎三角関数の基礎 ~sin・cos・tanとはそもそも何?
◎三角関数と正弦曲線の関係 ~sin波とcos波について
◎sinθの2乗 ~2の付く位置について
◎三角関数と象限 ~角度と符号の関係
◎正弦定理 ~三角形の辺と対角の関係
◎余弦定理 ~三角形の角と各辺の関係
◎加法定理とは? ~sin(α+β)の解法
◎積和の公式 ~sinαcosβなどの解法
◎和積の公式 ~sinα+sinβなどの解法
◎二倍角の公式 ~sin2αなどの解法
◎半角の公式 ~sin(α/2)の2乗などの解法
◎逆三角関数 ~アークサインやアークコサインとは?
