今回は、「三角関数と象限」についての説明です。
1.象限とは?
横軸x、縦軸yのグラフを描く時、x>0且つy>0の領域を第一象限、x<0且つy>0の領域を第二象限、x<0且つy<0の領域を第三象限、x>0且つy<0の領域を第四象限と呼びます。
一次関数とか出てきた辺りに習ったのではないでしょうか?
図で表すと以下のようになります。
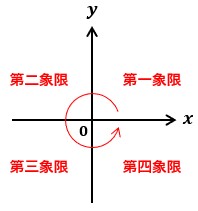
右上の領域を第一象限と覚えて、そこから反時計回りに第二象限、第三象限、第四象限と続くと覚えればいいと思います。
なんで象限と言うのかって?
知らんがな。
2.三角関数と象限の関係
三角関数と正弦曲線の関係の説明をする際に、横軸x、縦軸yとした時の原点を中心に単位円を描いて考えていきました。
なので、三角関数にも象限は関係してきます。
関係するといっても、象限に応じて符号が変化するだけですけどね。
各象限を角度θで表してみると、第一象限は0°<θ<90°、第二象限は90°<θ<180°、第三象限は180°<θ<270°、第四象限は270°<θ<360°に該当します。
sinθ、cosθ、tanθの各象限での符号をまとめると以下のような関係になります。
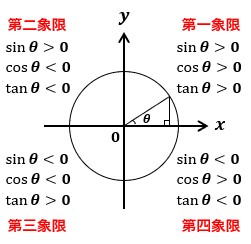
この関係だけ見ると困惑するかもしれませんが、冷静に考えれば当たり前のことしか書かれてません。
まず、ある角度θの時に単位円と交差する斜辺の大きさは”1″固定ですよね?
つまり、斜辺に関しては符号がプラスのまま変わらないわけです。
ここでsinθ、cosθ、tanθについて思い出してみてください。
sinθはy軸方向の長さを斜辺で割った値、cosθはx軸方向の長さを斜辺で割った値、tanθはy軸方向の長さをx軸方向の長さで割った値でした。
つまり、sinθの符号はy軸にのみ依存、cosθの符号はx軸にのみ依存、tanθの符号はx軸及びy軸の両方に依存することがわかります。
なので、sinθはy>0の領域である第一象限及び第二象限、cosθはx>0の領域である第一象限及び第四象限の時に符号がプラスになっているだけです。
tanθについても単純で、x軸とy軸の両方の符号が関係してくるので、x>0且つy>0のどちらの符号もプラスである第一象限とx<0且つy<0のどちらの符号もマイナスである第三象限の場合に符号がプラスになります。
以上の関係を図示しただけです。簡単でしょう?
3.象限を跨ぐ場合の符号の変化と公式
三角関数には公式が多々ありますが、特に名称が決められていない角度が変化した時の公式が存在します。
例えば、sin(θ+90°)=cosθといった公式です。
象限と三角関数の関係について触れてきたので、ついでにこれらの関係式についてもまとめておこうと思います。
なぜここにまとめるのかというと、θ+90°とは第一象限から第二象限、第二象限から第三象限のように象限を跨ぐことと同義だからです。
ということで、公式の紹介をしていきます。
sin(θ+90°)=cosθ
cos(θ+90°)=-sinθ
tan(θ+90°)=-(1/tanθ)
sin(180°-θ)=sinθ
cos(180°-θ)=-cosθ
tan(180°-θ)=-tanθ
『こんなに公式を覚えられない』と思うかもしれませんが、そもそも基本的に覚える必要はないです。
大切なのはなぜこうなるか、です。
ここで紹介した公式は図示してみれば自ずと導くことができるので、どちらかというとそのイメージの方が重要なのです。
まずは+90°の公式について考えてみましょう。
図3のように原点を中心に単位円を描き、角度θの△OABを形成します。
そしてもう一つ、角度がθ+90°の時の△OCDも描いてみます。
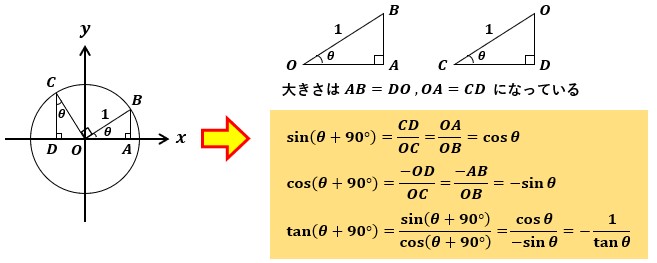
すると、∠CODは90°-θであることがわかるので、△OABと△OCDは斜辺の大きさが等しくその両端の角が等しいことから合同(同じ三角形)だと言えます。
ここで各辺の対応を考えていくと公式が導き出せるわけです。
角度が180°-θの場合も考え方は同じです。
実際に描いて確かめてみるわかりますが、左右対称の三角形ができるだけなのでx軸に関わる部分のみ符号が変わるとわかります。
以上、「三角関数と象限」についての説明でした。
【基礎から学ぶ三角関数】
◎三角関数の基礎 ~sin・cos・tanとはそもそも何?
◎三角関数と正弦曲線の関係 ~sin波とcos波について
◎sinθの2乗 ~2の付く位置について
◎三角関数と象限 ~角度と符号の関係
◎正弦定理 ~三角形の辺と対角の関係
◎余弦定理 ~三角形の角と各辺の関係
◎加法定理とは? ~sin(α+β)の解法
◎積和の公式 ~sinαcosβなどの解法
◎和積の公式 ~sinα+sinβなどの解法
◎二倍角の公式 ~sin2αなどの解法
◎半角の公式 ~sin(α/2)の2乗などの解法
◎逆三角関数 ~アークサインやアークコサインとは?
